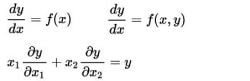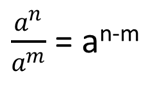Co to jest równanie?
Równanie w matematyce jest definiowane jako równość ustalona między dwoma wyrażeniami, w których może być jedna lub więcej niewiadomych do rozwiązania.
Równania służą do rozwiązywania różnych problemów matematycznych, geometrycznych, chemicznych, fizycznych lub jakichkolwiek innych, które mają zastosowanie w życiu codziennym, jak również w badaniach i rozwoju projektów naukowych.
Równania mogą mieć jedną lub więcej niewiadomych, a także może się zdarzyć, że nie mają rozwiązania lub że możliwe jest więcej niż jedno rozwiązanie.
Powiązane znaczenia:
Części równania
Równania składają się z różnych elementów. Przyjrzyjmy się każdemu z nich.
Każde równanie ma dwa człony , które są rozdzielone za pomocą znaku równości (=).
Każdy człon składa się z warunków , które odpowiadają każdemu z jednomianów.
Wartości każdego jednomianu w równaniu mogą mieć różny tenor. Na przykład:
-
(tixagag_4) stałe;
- współczynniki;
- zmienne;
- funkcje;
- wektory.
Niewiadome , czyli wartości, które chcą Państwo znaleźć, są reprezentowane przez litery. Popatrzmy na przykładowe równanie.
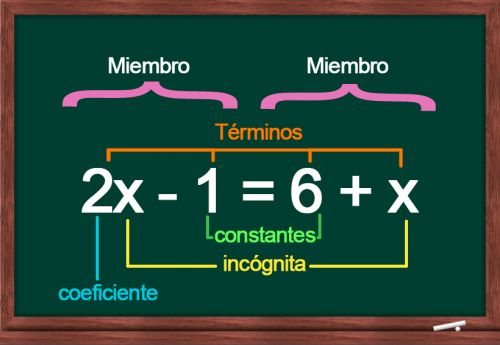Przykład równania algebraicznego
Rodzaje równań
Istnieją różne rodzaje równań w zależności od ich funkcji. Zobaczmy, jakie one są.
1. równania algebraiczne
Równania algebraiczne, które są podstawowymi równaniami, są sklasyfikowane lub podzielone na różne typy opisane poniżej.
a. Równania pierwszego stopnia lub równania liniowe
Są to takie, które obejmują jedną lub więcej zmiennych do pierwszej potęgi i nie przedstawiają iloczynu między zmiennymi.
Na przykład : a x + b = 0
Patrz także: Równanie pierwszego stopnia
b. Równania drugiego stopnia lub równania kwadratowe
W tym typie równania niewiadoma jest podniesiona do kwadratu.
Na przykład : ax2 + bx + c = 0
c. Równania trzeciego stopnia lub równania sześcienne
W tego typu równaniach nieznany człon jest podnoszony do sześcianu.
Na przykład : ax3+ bx2 + cx + d = 0
d. Równania czwartego stopnia
Takie, w których a, b, c i d są liczbami, które są częścią ciała, które może być albo 'a' albo 'b'.
Na przykład : ax4 + bx3 + cx2 + dx + e = 0
2. równania transcendentalne
Są one rodzajem równania, którego nie można rozwiązać wyłącznie za pomocą operacji algebraicznych, to znaczy, gdy zawiera ono przynajmniej jedną funkcję niealgebraiczną.
Na przykład
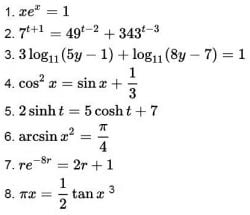
3. równania funkcyjne
Równania, których niewiadoma jest funkcją jednej zmiennej.
Na przykład
4. równania całkowe
Ten, w którym nieznana funkcja znajduje się w całce.
5. równania różniczkowe
Te, które odnoszą się do funkcji do jej pochodnych.
