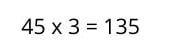Prawa wykładników i rodników ustalają uproszczony lub podsumowujący sposób opracowania serii operacji liczbowych z potęgami , które są zgodne z zestawem reguł matematycznych.
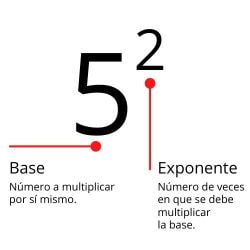
Wyrażenie an jest nazywane potęgą, (a) oznacza liczbę bazową, a (n lub nth) jest wykładnikiem, który wskazuje, ile razy podstawa powinna być pomnożona lub podniesiona zgodnie z tym, co jest wyrażone w wykładniku.
Prawo wykładników
Celem prawa wykładników jest podsumowanie wyrażenia liczbowego, które wyrażone w sposób kompletny i szczegółowy byłoby bardzo długie. Z tego powodu w wielu wyrażeniach matematycznych są one eksponowane jako potęgi.
Przykłady :
52 jest tym samym co (5) ∙ (5) = 25. To znaczy, że musi Pan pomnożyć 5 dwa razy.
23 jest takie samo jak (2) ∙ (2) ∙ (2) = 8. Czyli 2 musi być pomnożone trzy razy.
W ten sposób wyrażenie liczbowe jest prostsze i mniej kłopotliwe do rozwiązania.
1. potęga o wykładniku 0
Każda liczba podniesiona do wykładnika 0 jest równa 1. Należy zauważyć, że podstawa musi być zawsze różna od 0, tzn. ≠ 0.
Przykłady :
a0 = 1
-50 = 1
2. potęga o wykładniku 1
Każda liczba podniesiona do wykładnika 1 jest równa sobie.
Przykłady :
a1 = a
71 = 7
3. iloczyn potęg o równej podstawie lub mnożenie potęg o równej podstawie
Co jeśli mamy dwie równe podstawy (a) z różnymi wykładnikami (n)? To znaczy, ∙ am. W tym przypadku zachowane są równe podstawy i ich potęgi są sumowane, czyli: an ∙ am = an+m.
Przykłady :
22 ∙ 24 jest takie samo jak (2) ∙ (2) ∙ (2) x (2) ∙ (2) ∙ (2) ∙ (2) ∙ (2). To znaczy, że dodajemy wykładniki 22+4 i wynik byłby 26 = 64.
35 ∙ 3-2 = 35+(-2) = 35-2 = 33 = 27
Dzieje się tak, ponieważ wykładnik jest wskaźnikiem, ile razy liczba podstawowa musi być pomnożona przez siebie. Dlatego końcowy wykładnik będzie sumą lub odjęciem wykładników, które mają tę samą podstawę.
4. dzielenie potęg o tej samej podstawie lub iloraz dwóch potęg o tej samej podstawie
Iloraz dwóch potęg o równej podstawie jest równy podniesieniu podstawy o różnicę wykładników licznika minus mianownik. Podstawa musi być różna od 0.
Przykłady :
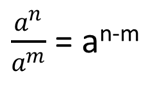
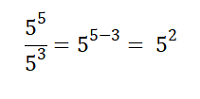
5. potęga iloczynu lub prawo rozdzielności potęgowania w odniesieniu do mnożenia
Prawo to mówi, że potęga iloczynu musi być podniesiona do tego samego wykładnika (n) w każdym z czynników.
Przykłady :
(a ∙ b ∙ c)n = an ∙ bn ∙ cn
(3 ∙ 5)3 = 33 ∙ 53 = (3 ∙ 3 ∙ 3 ∙ 3) (5 ∙ 5 ∙ 5) = 27 ∙ 125 = 3375.
(2ab)4 = 24 ∙ a4 ∙ b4 = 16 a4b4
6. Moc innej mocy
Odnosi się do mnożenia potęg o tych samych podstawach, z których otrzymuje się potęgę innej potęgi.
Przykłady :
(am)n = am∙n
(32)3 = 32∙3 = 36 = 729
7. prawo ujemnego wykładnika
Jeżeli mamy podstawę z ujemnym wykładnikiem (a-n), to musimy wziąć jednostkę podzieloną przez podstawę, która zostanie podniesiona ze znakiem wykładnika w plusie, czyli 1an . W tym przypadku podstawa (a) musi być różna od 0, a ≠ 0.
Przykład : 2-3 wyrażone jako ułamek wygląda jak:
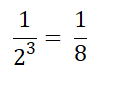
Mogą być Państwo zainteresowani prawami wykładników.
Prawa rodników
Prawo rodników jest operacją matematyczną, która pozwala nam znaleźć podstawę poprzez potęgę i wykładnik.
Radicals to pierwiastek kwadratowy, który wyraża się w następujący sposób √ i polega na tym, że otrzymujemy liczbę, która pomnożona przez siebie daje w wyniku to, co jest w wyrażeniu liczbowym.
Na przykład pierwiastek kwadratowy z 16 wyraża się w następujący sposób: √16 = 4; to znaczy, że 4,4 = 16. W tym przypadku nie jest konieczne podawanie wykładnika dwa w pierwiastku. Jednak w pozostałych korzeniach tak jest.
Na przykład:
Pierwiastek sześcienny z 8 wyraża się w następujący sposób: 3√8 = 2, tzn. 2 ∙ 2 ∙ 2 ∙ 2 = 8
Inne przykłady:
n√1 = 1, ponieważ każda liczba pomnożona przez 1 jest równa sobie.
n√0 = 0, ponieważ każda liczba pomnożona przez 0 jest równa 0.
1. prawo anulowania rodnika
Pierwiastek (n) podniesiony do potęgi (n) anuluje się.
Przykłady :
(n√a )n = a.
(√4 )2 = 4
(3√5 )3 = 5
2. pierwiastek z mnożenia lub iloczynu
Korzeń mnożenia można oddzielić jako mnożenie korzeni, niezależnie od rodzaju korzenia.
Przykłady :
![]()
![]()
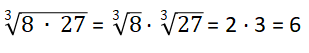
3. pierwiastek z dzielenia lub ilorazu
Pierwiastek z ułamka jest równy podziałowi pierwiastka z licznika i pierwiastka z mianownika.
Przykłady :
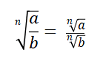
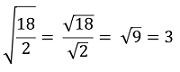
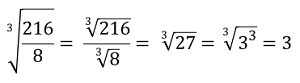
4. korzeń korzenia
Jeżeli korzeń znajduje się wewnątrz korzenia, to można pomnożyć indeksy obu korzeni, aby zredukować operację numeryczną do jednego korzenia, a radicand zostaje zachowany.
Przykłady :
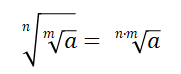
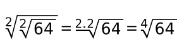
5. korzeń potęgi
Jeżeli w pierwiastku znajduje się liczba podniesiona o wykładnik, to jest ona wyrażona jako liczba podniesiona przez podzielenie wykładnika przez indeks pierwiastka.
Przykłady :
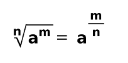
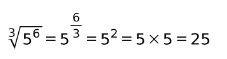
Patrz również Algebra.