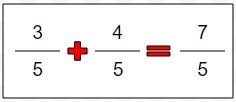
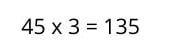Jakie są prawa wykładników?
Prawa wykładników to zbiór reguł ustalonych w celu rozwiązywania działań matematycznych z potęgami.
Potęga lub potęgowanie polega na wielokrotnym pomnożeniu liczby przez siebie i są przedstawiane graficznie w następujący sposób: xy.
Liczba, którą należy pomnożyć przez siebie, nazywa się podstawą, a liczba, przez którą należy ją pomnożyć, nazywa się wykładnikiem, który jest mniejszy i musi być umieszczony po prawej stronie i powyżej podstawy.
Na przykład
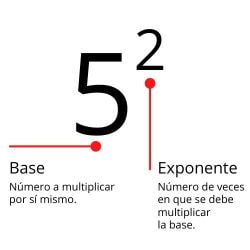
Jak teraz postępować przy operacjach dodawania, odejmowania, mnożenia i dzielenia z jedną lub kilkoma potęgami? Prawa wykładników prowadzą nas do rozwiązywania tych operacji w najprostszy możliwy sposób. Zobaczmy.
(tixagag_6) 1) Moc zerowa
1) Każda liczba podniesiona do 0 jest równa 1.
Na przykład
x0 = 1
50 = 1
370 = 1
2) Moc do 1
Każda liczba podniesiona do 1 jest równa samej sobie.
Na przykład
x1 = x
301 = 30
451 = 45
3) Mnożenie potęg o tej samej podstawie
Iloczyn potęg o identycznej podstawie jest równy potędze o takiej samej podstawie, podniesionej do sumy wykładników.
Na przykład
24 – 22 – 24 = 2(4 + 2 + 4) = 210
4) Podział potęg o tej samej podstawie
Przy dzieleniu potęg o tej samej podstawie i różnych wykładnikach, iloraz jest równy innej potędze o tej samej podstawie podniesionej do sumy wykładników.
Na przykład
44 : 42 = 4(4 – 2) = 42
5) Mnożenie potęg o tym samym wykładniku
Iloczyn dwóch lub więcej różnych potęg o tym samym wykładniku jest równy iloczynowi podstaw podniesionych do tego samego wykładnika.
Na przykład:
32 – 22 – 32 = (3 – 2 – 3)2 = 182
6) Dzielenie potęg o tym samym wykładniku
Z ilorazu dwóch potęg o różnych podstawach i równych wykładnikach wynika iloraz podstaw podniesionych do tego samego wykładnika.
Na przykład
82 : 22 = (8 : 2)2 = 42
7) Potęga potęgi
Z potęgi potęgi wynika inna potęga o tej samej podstawie podniesiona do iloczynu wykładników.
Na przykład:
(83)3 = 8(3 – 3) = 89
Mogą być Państwo również zainteresowani prawami wykładników i rodników.