Co to są prawa Keplera?
Prawa Keplera lub prawa ruchu planetarnego są prawami naukowymi, które opisują ruch planet wokół Słońca. Nazwę zawdzięczają swojemu twórcy, niemieckiemu astronomowi Johannesowi Keplerowi (1571-1630).
Podstawowym wkładem praw Keplera było wykazanie, że orbity planet są eliptyczne, a nie okrągłe, jak kiedyś sądzono.
W starożytności astronomia opierała się na teorii geocentrycznej , zgodnie z którą Słońce i planety krążyły wokół Ziemi. W XVI wieku Mikołaj Kopernik udowodnił, że planety krążą wokół Słońca, co zostało nazwane teorią heliocentryczną .
Chociaż teoria heliocentryczna zastąpiła teorię geocentryczną, obie miały wspólne przekonanie: że orbity planet są okrągłe. Dzięki odkryciu Keplera, teoria heliocentryczna mogła zostać udoskonalona.
Powiązane znaczenia:
Prawa Keplera są prawami kinetycznymi. Oznacza to, że ich funkcją jest opisywanie ruchu planetarnego, którego cechy charakterystyczne są wydedukowane dzięki matematycznym obliczeniom. Na podstawie tych informacji, wiele lat później Isaac Newton badał przyczyny ruchu planet.
Pierwsze prawo Keplera lub prawo orbit
Pierwsze prawo Keplera znane jest również jako „prawo orbit”. Określa on, że planety krążą wokół Słońca po eliptycznej orbicie. Słońce znajduje się w jednym z ognisk elipsy.
Stwierdzenie pierwszego prawa Keplera jest następujące:
Planety poruszają się eliptycznie wokół Słońca, które znajduje się w jednym z ognisk elipsy.
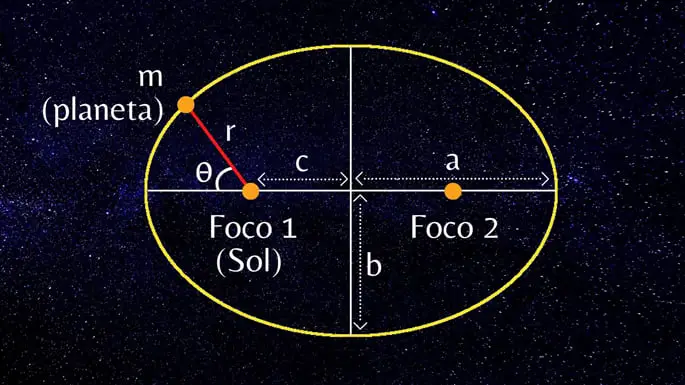(a) oś półmagor; (b) oś półmagor; (c) ognisko lub odległość od ogniska do środka; (r) wektor promienia lub odległość między punktem m (planeta) a ogniskiem 1 (Słońce); (
) kąt.
Elipsa jest zamkniętą krzywą, która ma dwie symetryczne osie, zwane ogniskami lub punktami stałymi. Prościej mówiąc, elipsę można opisać jako spłaszczone koło.
Stopień spłaszczenia zamkniętej krzywej nazywany jest ekscentrycznością . Gdy mimośród jest równy 0, krzywa tworzy idealny okrąg. Z drugiej strony, gdy mimośród jest większy niż 0, boki krzywej spłaszczają się i tworzą elipsę.
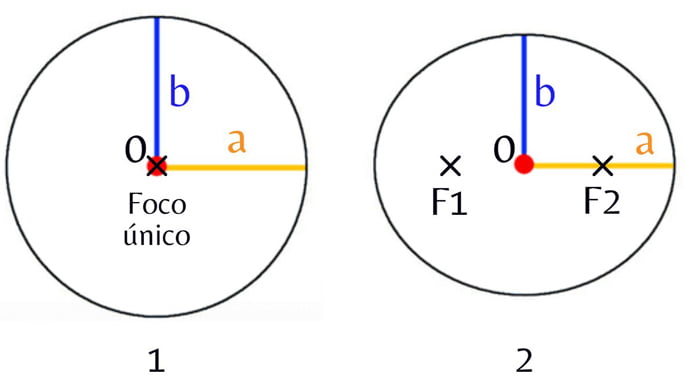1) Krzywa zamknięta o mimośrodzie 0 (koło); 2) Krzywa zamknięta o mimośrodzie 0,50 (elipsa).
Wzór do obliczania mimośrodu elipsy jest następujący:
gdzie,
- i jest mimośrodowością
- c jest odległością od ogniska do środka lub półodległości ogniskowej
- a jest osią półmajora
Na przykład, mimośród orbity Ziemi wynosi 0,0167. Oznacza to, że elipsa, którą opisuje Ziemia jest prawie okrągła.
Być może zainteresują Państwa: Ruch eliptyczny.
Drugie prawo Keplera lub prawo powierzchni
Drugie prawo Keplera znane jest jako „prawo powierzchni”. Stwierdza się, że wektor promieni omiata równoważne obszary w tym samym przedziale czasu.
Wektor promienia to wyobrażona linia łącząca planetę ze Słońcem. Dlatego jego długość zmienia się w zależności od odległości między nimi.
Stwierdzenie drugiego prawa Keplera jest następujące:
Wektor promienia łączący planetę ze Słońcem omiata równe obszary w równym czasie.
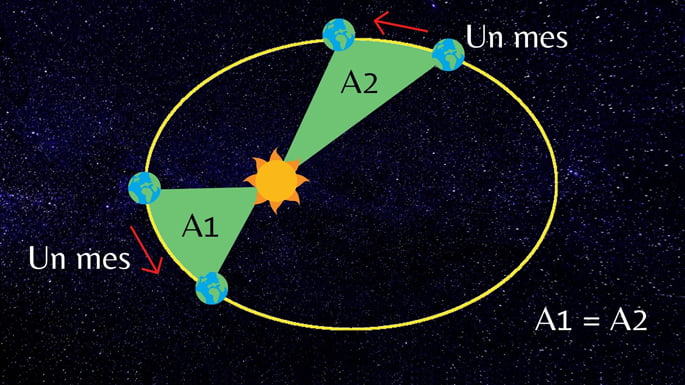
Czas, w którym wektor promienia przemieszcza się przez równoważne obszary nazywany jest prędkością areolarną . Ponieważ ten przedział jest zawsze taki sam, wnioskuje się, że prędkość areolowa jest stała.
Wynika z tego, że im dalej planeta jest od Słońca, tym wolniej się porusza. Im bliżej Słońca znajduje się planeta, tym szybciej się porusza.
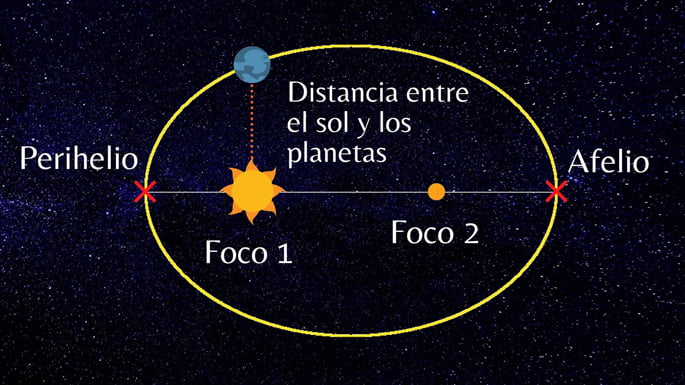
Istnieją dwa punkty na drodze planety, w których ciała niebieskie osiągają swoje graniczne odległości i prędkości. Te punkty nazywane są perihelion i aphelion.
peryhelium jest najbliższym punktem planety w stosunku do Słońca. W tym momencie planety rozwijają swoją maksymalną prędkość.
aphelium to najdalszy punkt między planetą a Słońcem. W tym momencie planety osiągają swoją minimalną prędkość.
Trzecie prawo Keplera lub prawo okresów
Trzecie prawo Keplera znane jest jako „prawo okresów” lub „prawo harmonii”. Dzięki temu można porównać cechy ruchu planet między sobą. W porównaniu uwzględnia się okres orbitalny i promień orbitalny każdej planety.
Okres orbitalny to czas, w którym planeta okrąża Słońce w całości. Promień orbity jest osią pół-majora elipsy.
Stwierdzenie trzeciego prawa Keplera jest następujące:
Kwadrat okresu orbitalnego każdej planety jest proporcjonalny do sześcianu promienia orbity.
Jeśli podzielimy kwadrat czasu orbitalnego przez sześcian promienia orbity, otrzymamy stałą, zwaną stałą Keplera. Stała Keplera jest taka sama dla wszystkich ciał niebieskich krążących wokół Słońca, ponieważ nie zależy od nich, lecz od masy słonecznej.
Formuła do obliczania trzeciego prawa Keplera jest następująca:
gdzie,
- T2 jest czasem orbitalnym lub okresem podniesionym do kwadratu
- a3 jest promieniem lub osią półmajora orbity sześciennej
- K jest stałą
Aby zilustrować to pytanie, w poniższej tabeli możemy porównać właściwości wszystkich planet, biorąc pod uwagę okres orbitalny (T) i promień orbity (a), aby otrzymać stałą Keplera (K). Okres orbitalny wyrażony jest w latach, a promień orbity w jednostkach astronomicznych (a.u.). Przyjrzyjmy się bliżej wartości K.
PlanetaT (años)a (u.a)KMercurio0,2410,3871,0002Venus0,6150,7231,000Tierra111,000Marte1,88811,5240,999Júpiter11,865,2040,997Saturno29,69,580,996Urano83,719,141,000Neptuno165,430,20,993
Jak widać w tabeli, wartość K jest praktycznie taka sama dla wszystkich planet. Różnica liczbowa jest niewielka. To mówi nam, że pomimo różnych właściwości planet, stosunek jest taki sam. Nazywamy to stałą Keplera.
Mogą być Państwo również zainteresowani:
- Prawa Newtona.
- Drugie prawo Newtona
