Co to jest płaszczyzna kartezjańska?
Płaszczyzna kartezjańska, współrzędne kartezjańskie lub układ kartezjański, to dwie prostopadłe linie liczbowe, jedna pozioma, a druga pionowa, które przecinają się w punkcie zwanym początkiem lub punktem zerowym.
Celem płaszczyzny kartezjańskiej jest opisanie pozycji lub położenia punktu na płaszczyźnie, który jest reprezentowany przez układ współrzędnych.
Płaszczyzna kartezjańska służy również do matematycznej analizy figur geometrycznych, takich jak parabola, hiperbola, prosta, obwód i elipsa, które są częścią geometrii analitycznej.
Nazwa płaszczyzny kartezjańskiej pochodzi od nazwiska francuskiego filozofa i matematyka René Descartes'a, który był twórcą geometrii analitycznej i pierwszym, który zastosował ten układ współrzędnych.
Części płaszczyzny kartezjańskiej
Elementy i cechy, które składają się na płaszczyznę kartezjańską to osie współrzędnych, początek, kwadranty i współrzędne. Tutaj objaśniamy każdy z nich.
Osie współrzędnych
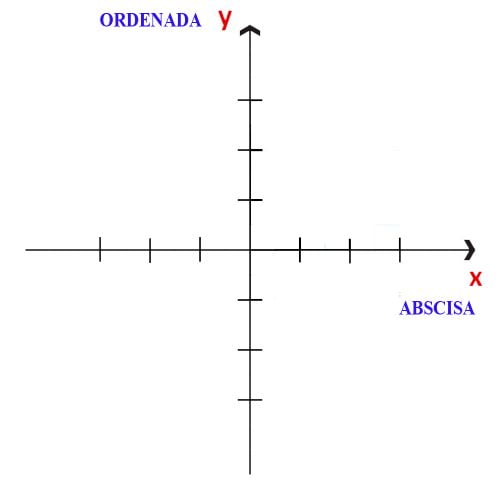
Dwie prostopadłe linie, które przecinają się w jednym punkcie na płaszczyźnie, nazywamy osiami współrzędnych. Te linie są nazywane odciętymi i rzędnymi.
-
(tixagag_4) Abscissa : Oś abscissa jest ułożona poziomo i jest oznaczona literą „x”.
- Rzędna : Oś rzędnych jest zorientowana pionowo i jest reprezentowana przez literę „y”.
Początek lub punkt 0
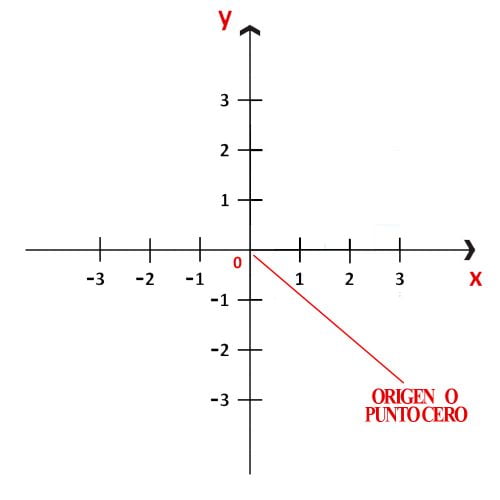
Punkt, w którym przecinają się osie „x” i „y” nazywany jest początkiem i przypisuje mu się wartość zero (0). Z tego powodu jest on również znany jako punkt zerowy (punkt 0). Każda oś reprezentuje skalę liczbową, która będzie dodatnia lub ujemna zgodnie z jej kierunkiem w stosunku do początku.
Tak więc, w odniesieniu do początku lub punktu 0, prawy odcinek osi „x” jest dodatni, podczas gdy lewy jest ujemny. W związku z tym odcinek wznoszący osi y jest dodatni, a odcinek opadający jest ujemny.
Kwadranty płaszczyzny kartezjańskiej
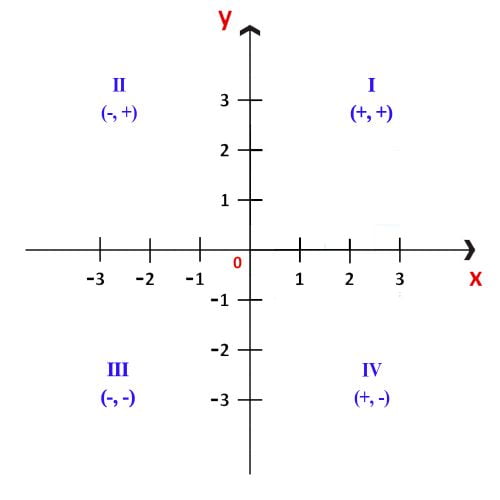
Cztery obszary utworzone przez połączenie dwóch prostopadłych linii nazywamy kwadrantami. Punkty płaszczyzny są opisane wewnątrz tych kwadrantów.
Kwadranty są tradycyjnie numerowane cyframi rzymskimi: I, II, III i IV.
- Kwadrant I : odcięta i rzędna są dodatnie.
- Kwadrant II : odcięta jest ujemna, a rzędna dodatnia.
- Kwadrant III : Zarówno odcięta jak i rzędna są ujemne.
- Kwadrant IV : odcięta jest dodatnia, a rzędna ujemna.
Może Panią/Pana również zainteresować: Geometria analityczna.
Współrzędne płaszczyzny kartezjańskiej
Współrzędne to liczby, które podają nam położenie punktu na płaszczyźnie. Współrzędne powstają poprzez przyporządkowanie pewnej wartości do osi „x” i innej wartości do osi „y”. Przedstawia się to w następujący sposób:
P (x, y), gdzie:
- P = punkt na płaszczyźnie;
(tixagag_4) x = oś abscissa (pozioma);
(tixagag_4) y = oś rzędnych (pionowa).
Jeżeli chcemy znać współrzędne punktu na płaszczyźnie, rysujemy prostą prostopadłą z punktu P do osi x – tę prostą nazywamy (ortogonalnym) rzutem punktu P na oś x.
Następnie rysujemy kolejną linię od punktu P do osi y – to jest rzut punktu P na oś y.
W każdym z przecięć rzutów z obiema osiami odzwierciedlona jest liczba (dodatnia lub ujemna). Te liczby to współrzędne.
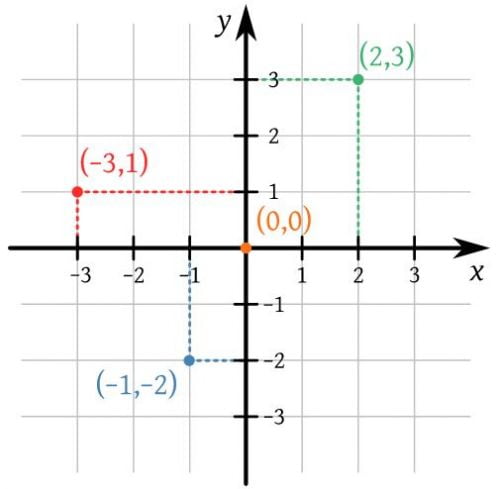
Na przykład
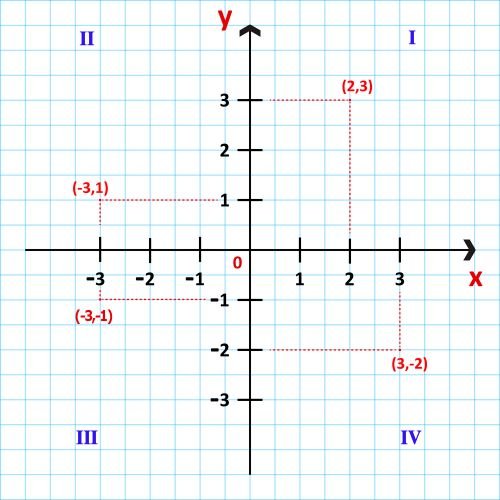
W tym przykładzie współrzędne punktów w każdym kwadrancie są następujące:
- kwadrant I, P (2, 3);
- kwadrant II, P (-3, 1);
- kwadrant III, P (-3, -1); oraz
- kwadrant IV, P (3, -2).
Jeżeli chcemy poznać położenie punktu na podstawie wcześniej przypisanych współrzędnych, to rysujemy prostą prostopadłą od wskazanego numeru abscissy, a kolejną od numeru ordinate. Przecięcie lub skrzyżowanie obu rzutów daje nam przestrzenne położenie punktu.
Na przykład
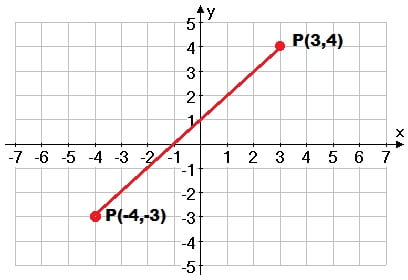
W tym przykładzie P (3,4) podaje nam dokładne położenie punktu w kwadrancie I płaszczyzny. 3 należy do osi odciętych, a 4 (prawy odcinek) do osi rzędnych (odcinek wznoszący).
P (-3,-4) daje nam konkretne położenie punktu w III kwadrancie płaszczyzny. Odcinek -3 należy do osi odciętych (odcinek lewy), a odcinek -4 do osi rzędnych (odcinek malejący).
Funkcje na płaszczyźnie kartezjańskiej
Funkcja przedstawiona jako: f(x)=y jest operacją mającą na celu uzyskanie ze zmiennej niezależnej (dziedzina) zmiennej zależnej (kontra dziedzina). Na przykład: f(x)=3x
Funkcja x
Domena
Domena Contra
f(2)=3x
2
6
f(3)=3x
3
9
f(4)=3x
4
12
Relacja dziedziny i przeciwdziedziny jest dwuwyrazowa , co oznacza, że ma tylko dwa poprawne punkty.
Aby znaleźć funkcję na płaszczyźnie kartezjańskiej musi Pan najpierw dokonać tabularyzacji, to znaczy ułożyć w tabeli znalezione pary punktów, aby później umieścić je lub zlokalizować na płaszczyźnie kartezjańskiej.
XYCoordenada23(2,3)-42(-4,2)6-1(6,-1)