Co to jest wektor?
W fizyce wektor jest odcinkiem linii w przestrzeni, który zaczyna się od jednego punktu i zmierza do innego, czyli ma kierunek i sens. Funkcją wektorów w fizyce jest wyrażanie tzw. wielkości wektorowych.
Termin wektor pochodzi od łacińskiego vector , vectoris , którego znaczenie to „to, co prowadzi” lub „to, co transportuje”.
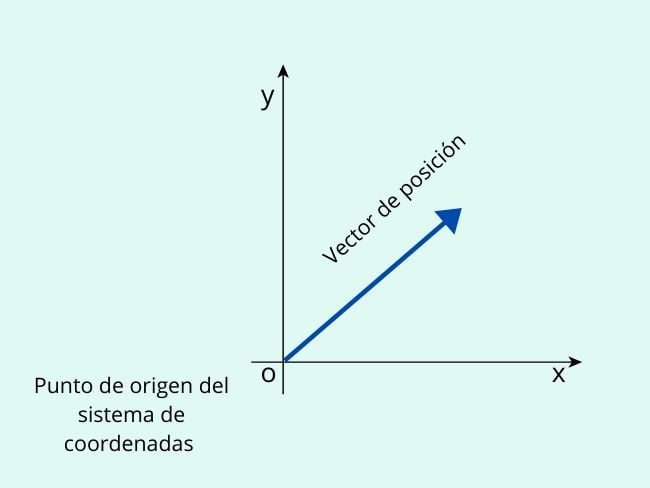
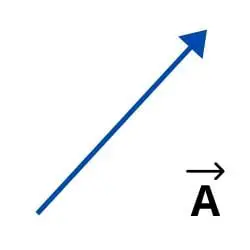
Wektory są przedstawiane graficznie za pomocą strzałki. Również, gdy mają być wyrażone w formule, są reprezentowane przez literę zakończoną strzałką.
Przykład 1:
E jexample 2:
![]()
Wielkości wektorowe
Wielkości wektorowe to takie wielkości, które oprócz tego, że są reprezentowane przez liczbę i jednostkę, muszą być również wyrażone w przestrzeni za pomocą kierunku i sensu, czyli za pomocą wektora. To odróżnia je od wielkości skalarnych, które wymagają tylko liczby i jednostki. Przykłady wielkości wektorowych są następujące:
- velocity;
- przesunięcie;
- przyspieszenie;
- impuls;
- siła;
- waga;
- moc;
- pole elektryczne;
- pole magnetyczne;
- pole grawitacyjne;
- energia cieplna;
- moment obrotowy;
- momentum .
Charakterystyka wektorów
Składowe wektorów, które definiują ich właściwości, są następujące:

-
(tixagag_4) Modulus lub magnitude: odnosi się do długości lub amplitudy wektora lub odcinka linii.
- Kierunek: odnosi się do nachylenia wektora w stosunku do urojonej osi poziomej, z którą tworzy on kąt.
- Kierunek: odnosi się do orientacji wektora, wskazanej przez grot strzałki wektora.
Typy wektorów
- Wektory zerowe: to takie, gdzie początek i koniec są zbieżne i dlatego moduł lub wielkość jest równa 0. Na przykład:

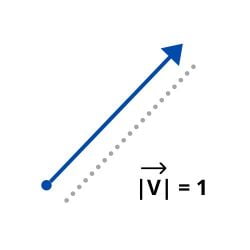
- Wektory jednostek: to takie, których modulus jest równy 1. Na przykład:

- Wektory stałe: to takie, które wyrażają punkt początkowy jak i końcowy, który jest określony w stałym punkcie w przestrzeni. Zazwyczaj używa się ich np. do wyrażenia siły przyłożonej do tego punktu. Aby je przedstawić, mówi się, że punktem początkowym jest A, a końcowym B. Na przykład:

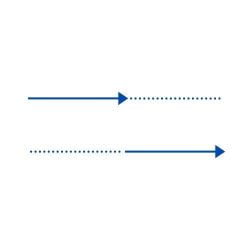
- Wektory równoległe: znajdują się na liniach równoległych, ale posiadają ten sam lub przeciwny kierunek. Na przykład:

- Przeciwne wektory: charakteryzują się tym, że mają ten sam kierunek i wielkość, ale ich sens jest przeciwny. Na przykład:

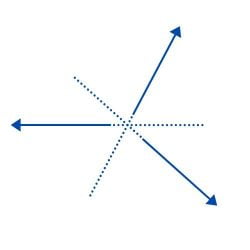
- Wektory współbieżne lub kątowe: to takie, których linie działania przechodzą przez ten sam punkt, czyli przecinają się. Na przykład:

- Wektory swobodne: to takie wektory, których punkt przyłożenia jest nieokreślony i dlatego swobodny. Na przykład:

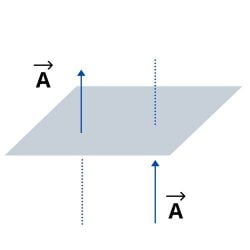
- Równorzędne lub równe wektory: to wektory o równym module, kierunku i zwrotności. Na przykład:

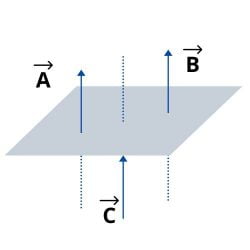
- Wektory współpłaszczyznowe: to te, które znajdują się w tej samej płaszczyźnie. Na przykład:

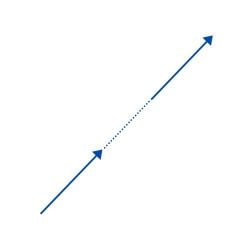
- Wektory współliniowe: ich linie działania leżą na tej samej linii. Na przykład:

- Wektory osiowe lub pseudowektory: to te, które są związane z efektami rotacyjnymi. Kierunek wskazuje na oś obrotu segmentu. Na przykład:

Wektor w matematyce
W matematyce, w dziedzinie rachunku wektorowego, wektor jest zorientowanym odcinkiem linii, który zależy od układu współrzędnych, na którym można wykonać ważną liczbę operacji, takich jak dodawanie, odejmowanie, rozkład, kąt między dwoma wektorami itp.
Wektor w zdrowiu
W medycynie wektor to każda żywa i organiczna istota zdolna do przenoszenia wirusów, bakterii, grzybów lub pasożytów z zainfekowanej istoty do zdrowej. Na przykład: komar Aedes Aegypti jest wektorem dengi i żółtej febry, tzn. jest odpowiedzialny za przenoszenie czynnika, który przenosi chorobę.