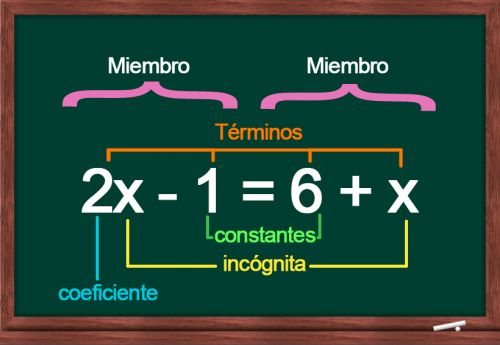
Równanie pierwszego stopnia jest matematyczną równością z jedną lub więcej niewiadomymi . Te niewiadome muszą być usunięte lub rozwiązane, aby znaleźć wartość liczbową równości.
Równania pierwszego stopnia są tak nazywane, ponieważ ich zmienne (niewiadome) są podniesione do pierwszej potęgi (X1) , która jest zwykle reprezentowana tylko przez X.
Podobnie stopień równania wskazuje na liczbę możliwych rozwiązań. Dlatego równanie pierwszego stopnia (zwane również równaniem liniowym) ma tylko jedno rozwiązanie.
Równanie pierwszego stopnia z jedną niewiadomą
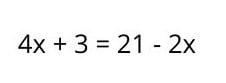
Aby rozwiązać równania liniowe z jedną niewiadomą, należy wykonać kilka kroków:
Proszę zgrupować terminy z X w pierwszym członie , a te bez X w drugim członie. Ważne jest, aby pamiętać, że kiedy termin przechodzi na drugą stronę równości, zmienia się jego znak (jeśli jest dodatni, staje się ujemny i odwrotnie).
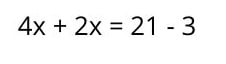
3. Proszę wykonać odpowiednie operacje na każdym członie równania. W tym przypadku w jednym z członów jest dodawanie, a w drugim odejmowanie, co daje wynik:

4. Wyczyścić X , przenosząc termin przed nim na drugą stronę równania, z przeciwnym znakiem. W tym przypadku terminem jest mnożenie, a więc teraz dzielenie.
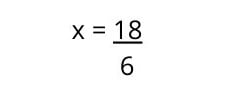
5. Proszę rozwiązać działanie , aby znaleźć wartość X.
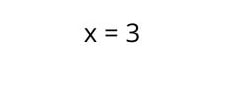
Wtedy rozwiązanie równania pierwszego stopnia byłoby następujące:
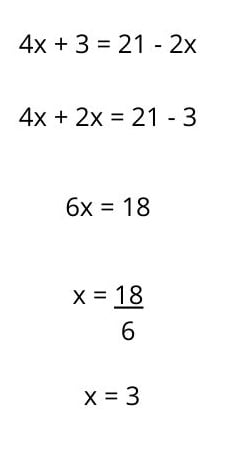
Równanie pierwszego stopnia z nawiasem
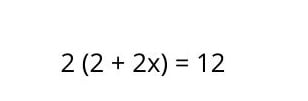
W równaniu liniowym z nawiasami znaki te mówią nam, że wszystko, co znajduje się wewnątrz nich, musi być pomnożone przez liczbę przed nimi. To jest krok po kroku do rozwiązywania tego typu równań:
1. Pomnożyć termin przez wszystko wewnątrz nawiasu , tak by równanie wyglądało następująco:
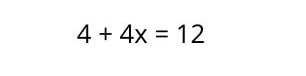
2. Po rozwiązaniu mnożenia pozostaje nam równanie pierwszego stopnia z niewiadomą , które rozwiązuje się tak jak wcześniej, czyli grupując wyrazy i wykonując odpowiednie operacje, zmieniając znaki tych wyrazów, które przechodzą na drugą stronę równości:
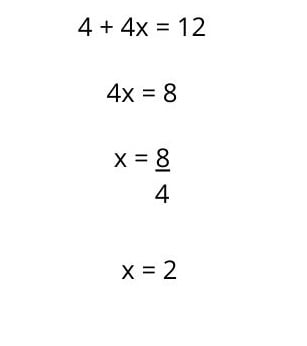
Równanie pierwszego stopnia z ułamkami i nawiasami
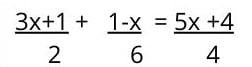
Chociaż równania pierwszego stopnia z ułamkami wyglądają na skomplikowane, w rzeczywistości wymagają tylko kilku dodatkowych kroków, zanim staną się równaniem podstawowym:
1. Najpierw musimy otrzymać najmniejszą wspólną wielokrotność mianowników (najmniejsza wielokrotność, która jest wspólna dla wszystkich obecnych mianowników). W tym przypadku najmniejszą wspólną wielokrotnością jest 12.
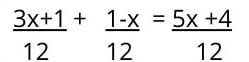
2. Następnie należy podzielić wspólny mianownik przez każdy z oryginalnych mianowników . Otrzymany w ten sposób iloczyn pomnoży licznik każdego z ułamków, które są teraz ujęte w nawiasy.
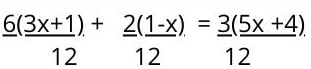
3. Proszę pomnożyć iloczyny przez każdy z członów wewnątrz nawiasu , tak jak w przypadku równania pierwszego stopnia z nawiasem.
Na końcu równanie upraszcza się przez usunięcie wspólnych mianowników:
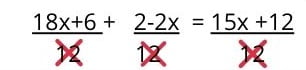
Wynikiem jest równanie pierwszego stopnia z jedną niewiadomą, które rozwiązuje się w zwykły sposób:
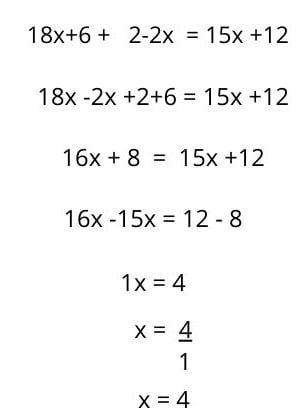
Patrz także: Algebra.